Le terne pitagoriche
Il teorema di Pitagora
Definizione di terna
pitagorica
Terne primitive e terne derivate
Esploriamo il mondo delle
terne pitagoriche (Javascript)
Alcune osservazioni in ordine
sparso
Immagini
Esiste una formula che permette di trovare tutte le terne
pitagoriche?
Il teorema di Pitagora.
Il teorema di Pitagora afferma
che:
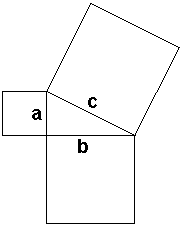
In un triangolo rettangolo la somma dei quadrati costruiti sui cateti
è uguale al quadrato costruito sull'ipotenusa.
 |
In Algebra, il teorema di Pitagora può essere espresso
così:
Se a e b sono i cateti di un triangolo rettangolo e c è l'ipotenusa,
si ha che:a2 + b2 =
c2
Definizione di terna pitagorica.
Se tre numeri interi a, b e c verificano la relazione a2 + b2 = c2, si dice che formano una terna pitagorica.
Ad esempio (3, 4, 5) e (5, 12, 13) sono due notissime terne pitagoriche, mentre non lo è (1, 1, radq(2)) perché l'ultimo numero non è intero.
Anche (6, 8, 10) è una terna pitagorica, ottenuta raddoppiando i termini della (3, 4, 5).
Terne primitive e terne derivate.
Le terne come la (3, 4, 5) sono dette terne primitive e quelle come la (6, 8, 10) sono dette derivate.
Infatti, se (a, b, c) è una terna pitagorica, lo è anche (ka, kb, kc), con k numero intero positivo.Come si distinguono le terne primitive da quelle derivate?
Semplice: se a e b sono primi fra loro allora la terna è primitiva, altrimenti è derivata.
Esploriamo il mondo delle terne pitagoriche
Prima di procedere potete esplorare il mondo delle terne con questo piccolo programmino in Javascript che gira nel riquadro qui sotto.
Che cosa osservate?
N.B. Il programma fuziona anche off-line, basta salvare questa pagina.
Alcune osservazioni, in ordine sparso
In tutte le terne pitagoriche:
- uno dei tre "lati" a, b, c è divisibile per 3 e un altro per 5
- il prodotto dei due "cateti" a*b è divisibile per 12
- il prodotto dei tre "lati" a*b*c è divisibile per 60Nelle terne pitagoriche primitive:
- uno dei due "cateti" a oppure b è pari e l'altro dispari, mentre l'"ipotenusa" c è sempre dispari
- a, b sono primi fra loro
Immagini
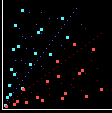
Se disegniamo nel piano cartesiano i punti di coordinate (a, b) tali che a,
b, radq(a2 + b2) sia una terna pitagorica, otteniamo
immagini come le seguenti.I punti che individuano le coppie (a,b) sono
simmetrici rispetto alla bisettrice del primo quadrante.
Le coppie (a,b) che
appartengono a terne primitive sono colorate in celeste e rosa.
Le
coppie (a,b) che individuano terne derivate sono colorate in blu e
rosso.
I cateti delle terne pitanel quadrato di lato 100 |
|
|
pie (a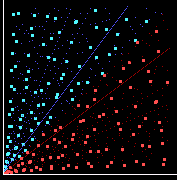
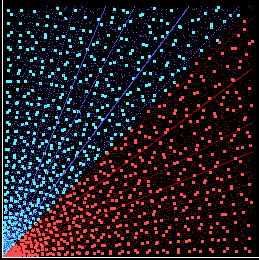grandi rappresentano le terne primitive,